Bab 3

Hana




BAB III

Implementasi Algoritma Genetika dalam MATLAB



1. Sekilas tentang MATLAB [BACK] 
    
    MATLAB berasal dari singkatan MATrix LABoratory, dimana aplikasi ini akan memudahkan pengguna dalam operasi matriks, terutama dalam pengimplementasiannya ke GA.
          


  • Pemograman MATLAB  [BACK] 
    • Dalam MATLAB, setiap variabel dianggap sebagai matriks.
    • Pembuatan program atau fungsi dalam MATLAB dapat dilakukan dengan file berekstensi .m. (nama fungsi harus sama dengan nama file)
    • MATLAB bersifat case sensitive, sehingga antara "A" dan "a" akan dibaca sebagai dua variabel yang berbeda.
    • i dan j merupakan tanda bilangan imajiner, sehingga perlu dihindari menggunakan variabel j dan i.
  • Matriks
    • Merupakan sekumpulan angka berbentuk persegi.
  • Sum, Transpose, dan diag
    • Sum



    • Transpose
  • Diag
  • Indeks Matriks
    • Penunjukan elemen matrik dapat dilakukan dengan berdasarkan indeksnya.
    • Remember! : Matriks(baris,kolom)
    • Contoh kasus :


  • Operator ":"
    • Penanda deret bilangan bulat
                   ":" menyatakan bahwa deretan merupakan bilangan bulat dengan kelipatan 1

                   ":" menyatakan bahwa deretan merupakan bilangan bulat dengan kelipatan -5

                   ":" menyatakan bahwa C berisi elemen vektor B baris 1 hingga baris 3

.
  • Membangkitkan Matriks
    • zeros (semua nol)
    • ones (semua satu)
    • rand (random dalam distribusi uniform)
    • randn (random dalam distribusi normal)

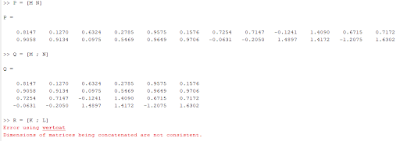
  • Concatenation
    • Penggabungan beberapa matrik kecil menjadi sebuah matriks besar
    • Untuk menggabungkan matriks berdasarkan kolom, digunakan ";" 
    • Untuk menggabungkan matriks berdasarkan baris, tidak perlu ada ";"
    • Jika matriks yang digabung memiliki jumlah baris/kolom yang berbeda, makan akan muncul error.

  • Operasi-operasi Matriks
    • + (penjumlahan)
    • - (pengurangan)
    • *(perkalian matriks)
    • .*(perkalian elemen per elemen)
    • ./ (pembagian elemen per elemen, variabel kiri dibagi kanan)
    • .\ (pembagian elemen per elemen, variabel kanan dibagi kiri)
    • .^ (perpangkatan elemen per elemen)





2. Implementasi Algoritma Genetika [BACK] 
    
    Pada penjelasan berikut akan diterapkan GA untuk mencari nilai dari fungsi h:

        Tujuan fungsi ini untuk membangkitkan populasi yang berisi sejumlah kromosom.

    Hasil akhir berupa Populasi dengan matriks berukuran 200 x 20, di mana setiap elemen adalah 0 atau 1. Matriks ini sering digunakan dalam konteks algoritma genetik atau studi lain di mana populasi individu (baris-baris dalam matriks) diwakili oleh gen-gen (kolom-kolom dalam matriks), dan setiap gen bisa bernilai 0 atau 1.

          Bertujuan untuk mengodekan sebuah kromosom yang berisi bilangan biner menjadi individu x yang bernilai real dalam interval yang diinginkan, berdasarkan persamaan berikut:

Proses Dekode:

  1. Inisialisasi Loop Variabel:

    for ii = 1:Nvar
      x(ii) = 0;
    • Loop pertama mengiterasi melalui setiap variabel ii dari 1 hingga Nvar. Untuk setiap variabel, kita akan menghitung nilai real yang sesuai dari bagian kromosom yang mengkodekan variabel tersebut.

  2. Dekode Kromosom:

    for jj = 1:Nbit
      x(ii) = x(ii) + Kromosom((ii-1)*Nbit+jj) * 2^(-jj);
    end
    • Loop kedua mengiterasi melalui setiap bit jj dari 1 hingga Nbit. Untuk setiap bit, kita mengakumulasi nilai biner yang terkode dalam variabel x(ii):
      • Kromosom((ii-1)*Nbit+jj) mengambil bit ke-jj dari kromosom yang mengkodekan variabel ke-ii.
      • 2^(-jj) mengonversi bit ke-jj menjadi nilai desimal sesuai posisinya dalam sistem biner.
      • Dengan menambahkan nilai ini ke x(ii), kita membangun representasi desimal dari bit-bit biner.

  3. Transformasi ke Rentang Real:

    x(ii) = Rb + (Ra - Rb) * x(ii);
    • Setelah mendapatkan nilai desimal dari bit biner, kita mengubahnya ke dalam rentang [Rb, Ra] dengan menggunakan rumus:
      • Rb + (Ra - Rb) * x(ii)
      • Di sini, x(ii) berada dalam rentang [0, 1] setelah dekode biner, dan rumus ini mengubahnya ke rentang [Rb, Ra].

Contoh Penggunaan:

Misalnya, jika Kromosom adalah [1 0 1 1 0 0 1 0], Nvar adalah 2, Nbit adalah 4, Ra adalah 10, dan Rb adalah 5, maka:

  1. Untuk variabel pertama (4 bit pertama), kromosom [1 0 1 1] diubah menjadi nilai desimal 1*(2^(-1)) + 1*(2^(-2)) + 0*(2^(-3)) + 1*(2^(-4)) = 0.8125.
  2. Nilai ini kemudian diubah ke rentang [5, 10]:
    • 5 + (10 - 5) * 0.8125 = 5 + 5 * 0.8125 = 5 + 4.0625 = 9.0625.

Hasil Akhir:

Fungsi ini mengembalikan x, sebuah vektor yang berisi nilai real hasil dekode dari setiap variabel dalam kromosom, sesuai dengan rentang yang ditentukan.


Fungsi DekodekanKromosom mengubah kromosom biner menjadi nilai real dalam rentang tertentu dengan mengonversi setiap bagian dari kromosom yang mewakili variabel menjadi angka desimal, kemudian menskalakannya ke dalam rentang [Rb, Ra].

  1. Kromosom Generation:

    Kromosom = randi([0 1], 1, 20);
    • randi([0 1], 1, 20) menghasilkan vektor baris Kromosom yang berisi 20 bilangan biner (0 atau 1) secara acak. Ini adalah kromosom biner yang akan didekodekan.
    • Contoh hasilnya bisa berupa: [1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 1 1].

  2. Parameter Dekode:

    Nvar = 2;
    Nbit = 10;
    Ra = 5.12;
    Rb = -5.12;
    • Nvar: jumlah variabel yang ingin didekodekan
    • Nbit: jumlah bit yang mengkodekan setiap variabel
    • Ra: batas atas rentang nilai real yang diinginkan untuk variabel
    • Rb: batas bawah rentang nilai real yang diinginkan untuk variabel

  3. Panggilan Fungsi DekodekanKromosom:

    x = DekodekanKromosom(Kromosom, Nvar, Nbit, Ra, Rb);
    • Fungsi DekodekanKromosom akan mengubah kromosom biner Kromosom menjadi nilai real sesuai dengan parameter Nvar, Nbit, Ra, dan Rb.

Proses Dekode

Fungsi DekodekanKromosom mengonversi kromosom biner menjadi nilai real dalam rentang [Rb, Ra] dengan langkah-langkah berikut:

  1. Inisialisasi Hasil Dekode:

    x(ii) = 0;
    • Untuk setiap variabel (dalam hal ini ada 2 variabel), x(ii) diinisialisasi ke 0.

  2. Dekode Bit ke Desimal:

    for jj = 1:Nbit
      x(ii) = x(ii) + Kromosom((ii-1)*Nbit + jj) * 2^(-jj);
    end
    • Untuk setiap bit dalam kromosom yang mewakili variabel, bit-bit ini dikonversi menjadi nilai desimal berdasarkan posisi bit dalam bilangan biner.
    • Contohnya, jika variabel pertama mengacu pada 10 bit pertama dari Kromosom, maka fungsi ini mengonversi 10 bit tersebut menjadi nilai desimal antara 0 dan 1.

  3. Transformasi ke Rentang Real:

    x(ii) = Rb + (Ra - Rb) * x(ii);
    • Setelah mendapatkan nilai desimal dari bit biner, nilai ini diubah ke dalam rentang [Rb, Ra] dengan menggunakan rumus linear:
      • x(ii) = Rb + (Ra - Rb) * x(ii)
      • Ini menskalakan nilai desimal ke dalam rentang yang diinginkan.

Contoh Penghitungan

Misalkan Kromosom adalah [1 0 1 0 1 1 0 1 0 0 1 0 0 1 0 1 1 0 1 1]. Untuk Nvar = 2 dan Nbit = 10:

  • Variabel Pertama:
    • Mengambil 10 bit pertama dari Kromosom: [1 0 1 0 1 1 0 1 0 0]
    • Menghitung nilai desimal dari bit ini.
    • Misalkan hasil desimalnya adalah 0.6234 (hanya contoh, hasil aktual akan bergantung pada bit).

    • Mengubah nilai desimal ke rentang [Rb, Ra]:

      x(1) = -5.12 + (5.12 - (-5.12)) * 0.6234 = -5.12 + 10.24 * 0.6234 ≈ -5.12 + 6.39 ≈ 1.27
  • Variabel Kedua:
    • Mengambil 10 bit berikutnya dari Kromosom: [0 1 0 0 1 0 1 0 1 1]
    • Menghitung nilai desimal dan mengubahnya ke rentang yang sama dengan proses di atas.


Hasil Akhir:

Vektor x berisi dua nilai real yang merupakan hasil dekode dari dua variabel biner dari kromosom biner ke rentang [Rb, Ra].


          Fungsi ini bertujuan untuk menghitung nilai fitness dari suatu individu x

  1. Parameter:

    • x: Vektor yang berisi nilai-nilai individu yang akan dievaluasi. Dalam konteks ini, x diharapkan sebagai vektor dengan setidaknya dua elemen (misalnya x = [x1, x2]), di mana x1 dan x2 adalah nilai-nilai yang diperoleh dari proses dekode kromosom atau input lain.
    • BilKecil: Parameter tambahan yang digunakan untuk menghindari nilai fitness menjadi terlalu kecil. Biasanya, BilKecil adalah nilai kecil positif yang ditambahkan untuk menghindari pembagi nol atau nilai fitness yang terlalu kecil.

  2. Fungsi Fitness:

    fitness = 1 / ((1000 * (x(1) - 2 * x(2))^2 + (1 - x(1))^2) + BilKecil);
    • Fungsi fitness dihitung dengan formula:
      fitness = 1 / (f(x) + BilKecil)
      Di mana f(x) adalah fungsi objektif yang dinyatakan dalam kurung:
      f(x) = 1000 * (x(1) - 2 * x(2))^2 + (1 - x(1))^2


Interpretasi Fungsi Fitness

  1. Fungsi Objektif f(x):

    • f(x) adalah fungsi kuadrat yang dihitung dari elemen-elemen vektor x:
      • 1000 * (x(1) - 2 * x(2))^2: Mengukur seberapa jauh kombinasi x(1) dan x(2) dari kondisi ideal x(1) = 2 * x(2).
      • (1 - x(1))^2: Mengukur seberapa jauh x(1) dari nilai ideal 1.
    • Fungsi ini biasanya digunakan dalam masalah optimasi di mana kita ingin meminimalkan nilai f(x).

  2. Penambahan BilKecil:

    • BilKecil ditambahkan pada penyebut untuk menghindari pembagi nol atau menghindari nilai fitness yang menjadi sangat besar jika f(x) mendekati nol.
    • Ini membantu memastikan bahwa fitness tetap dalam rentang yang dapat diterima dan stabil selama evaluasi.

  3. Fitness Function:

    • Fitness didefinisikan sebagai invers dari nilai f(x) + BilKecil:
      • Ketika f(x) rendah (mendekati nol), fitness akan tinggi, yang berarti individu tersebut dianggap baik.
      • Ketika f(x) tinggi, fitness akan rendah, yang menunjukkan individu tersebut kurang baik.

Contoh:

Misalkan x = [1.5, 0.5] dan BilKecil = 1e-6:

  1. Hitung f(x):

    f(x) = 1000 * (1.5 - 2 * 0.5)^2 + (1 - 1.5)^2
         = 1000 * (1.5 - 1)^2 + (-0.5)^2
         = 1000 * (0.5)^2 + 0.25
         = 1000 * 0.25 + 0.25
         = 250 + 0.25
         = 250.25

  2. Hitung fitness:

    fitness = 1 / (250.25 + 1e-6)
            ≈ 1 / 250.250001
            ≈ 0.00399

            Untuk menjaga individu dengan nilai fitness terbaik, maka dilakukan elitisme,


BilKecil = 0.1;
fitness = EvaluasiIndividu(x, BilKecil);
  • BilKecil diatur sebagai 0.1, digunakan untuk stabilisasi dalam fungsi fitness EvaluasiIndividu.
  • fitness menghitung fitness individu x menggunakan parameter BilKecil.

x = DekodekanKromosom(Populasi(1,:), Nvar, Nbit, Ra, Rb);
Fitness(1) = EvaluasiIndividu(x, BilKecil);
MaxF = Fitness(1);
MinF = Fitness(1);
IndeksIndividuTerbaik = 1;
  • Mengambil kromosom pertama dari Populasi dan mendekodifikasinya ke nilai real x dengan DekodekanKromosom.
  • Menghitung fitness dari individu tersebut dan menyimpannya dalam Fitness(1).
  • MaxF dan MinF diinisialisasi dengan fitness individu pertama, sehingga saat ini MaxF dan MinF sama dengan fitness individu pertama.
  • IndeksIndividuTerbaik diatur ke 1, menandakan bahwa individu pertama adalah yang terbaik saat ini.

for ii = 2:UkPop
    Kromosom = Populasi(ii, :);
    x = DekodekanKromosom(Kromosom, Nvar, Nbit, Ra, Rb);
    Fitness(ii) = EvaluasiIndividu(x, BilKecil);
    if (Fitness(ii) > MaxF)
        MaxF = Fitness(ii);
        IndeksIndividuTerbaik = ii;
        BestX = x;
    end
    if (Fitness(ii) < MinF)
        MinF = Fitness(ii);
    end
end
  • Loop ini iterasi melalui setiap individu dalam populasi dari ii = 2 hingga UkPop.
  • Untuk setiap individu:
    • Ambil kromosom individu dan dekode menjadi nilai real x.
    • Hitung fitness individu tersebut dan simpan di Fitness(ii).
    • Jika fitness individu lebih tinggi dari MaxF, update MaxF dan IndeksIndividuTerbaik, serta simpan x sebagai BestX (individu terbaik).
    • Jika fitness individu lebih rendah dari MinF, update MinF.

TemPopulasi = Populasi;
if mod(UkPop, 2) == 0
    IterasiMulai = 3;
    TemPopulasi(1, :) = Populasi(IndeksIndividuTerbaik, :);
    TemPopulasi(2, :) = Populasi(IndeksIndividuTerbaik, :);
else
    IterasiMulai = 2;
    TemPopulasi(1, :) = Populasi(IndeksIndividuTerbaik, :);
end
  • TemPopulasi adalah salinan dari Populasi yang mungkin akan digunakan dalam iterasi berikutnya atau untuk tujuan lain dalam algoritma.
  • Cek apakah UkPop (ukuran populasi) adalah genap dengan mod(UkPop, 2) == 0:
    • Jika genap, set IterasiMulai ke 3. Salin individu terbaik ke baris pertama dan kedua dari TemPopulasi.
    • Jika tidak genap, set IterasiMulai ke 2. Salin individu terbaik ke baris pertama dari TemPopulasi.

          Untuk menghindari kecenderungan konvergen pada optimum lokal, maka digunakan penskalaan nilai fitness yang bertujuan untuk mendapatkan nilai fitness yang lebih baik, bervariansi tinggi.

Fungsi LinearFitnessRanking ini digunakan dalam algoritma genetik untuk melakukan pemeringkatan individu berdasarkan nilai fitness mereka. Tujuan dari fungsi ini adalah untuk menyesuaikan fitness individu dengan skala linear sehingga individu dengan fitness lebih tinggi mendapatkan nilai fitness yang lebih tinggi dalam skala baru, sedangkan individu dengan fitness lebih rendah mendapatkan nilai fitness yang lebih rendah. Fungsi ini membantu dalam pemilihan individu untuk proses reproduksi.

function LFR = LinearFitnessRanking(UkPop, Fitness, MaxF, MinF)
  • UkPop: Jumlah individu dalam populasi.
  • Fitness: Vektor yang berisi nilai fitness asli dari setiap individu dalam populasi.
  • MaxF: Nilai fitness maksimum yang diinginkan dalam skala baru.
  • MinF: Nilai fitness minimum yang diinginkan dalam skala baru.


Proses dalam Fungsi

  1. Mengurutkan Fitness:

    [SF, IndF] = sort(Fitness);
    • SF adalah vektor nilai fitness yang telah diurutkan dari yang terkecil hingga terbesar.
    • IndF adalah indeks yang menunjukkan urutan dari nilai fitness dalam vektor asli.
    • IndF digunakan untuk mengetahui posisi individu dalam urutan fitness yang telah diurutkan.

  2. Penyesuaian Fitness Linear:

    for rr = 1:UkPop
      LFR(IndF(UkPop - rr + 1)) = MaxF - (MaxF - MinF) * ((rr - 1) / (UkPop - 1));
    end
  • LFR adalah vektor hasil yang berisi nilai fitness baru berdasarkan skala linear.
  • Loop for rr = 1:UkPop mengiterasi melalui setiap individu dalam populasi.
    • rr adalah iterasi saat ini, yang juga menunjukkan urutan individu dalam daftar SF (fitness terurut).
    • IndF(UkPop - rr + 1) mendapatkan indeks individu asli yang sesuai dengan urutan fitness rr.
    • LFR(IndF(UkPop - rr + 1)) mengatur fitness baru untuk individu tersebut.

    Skala Linear:
  • Nilai fitness baru dihitung dengan rumus:
    LFR(IndF(UkPop - rr + 1)) = MaxF - (MaxF - MinF) * ((rr - 1) / (UkPop - 1))
  • Rumus ini mengubah fitness asli menjadi nilai baru yang terdistribusi secara linear antara MaxF (fitness maksimum) dan MinF (fitness minimum).
  • Individu dengan fitness terbaik mendapatkan nilai mendekati MaxF, sedangkan individu dengan fitness terburuk mendapatkan nilai mendekati MinF.

Contoh

Misalkan kita memiliki 5 individu dalam populasi dengan fitness yang diukur sebagai berikut:

  • Fitness: [10, 15, 20, 25, 30]
  • UkPop: 5
  • MaxF: 1.0
  • MinF: 0.0

Langkah-langkah dalam fungsi:

  1. Urutkan Fitness:

    • SF = [10, 15, 20, 25, 30]
    • IndF = [1, 2, 3, 4, 5] (indeks asli)

  2. Hitung Fitness Linear:

    • Untuk rr = 1: LFR(IndF(5 - 1 + 1)) = LFR(5) = MaxF - (MaxF - MinF) * ((1 - 1) / (4)) = 1.0
    • Untuk rr = 2: LFR(IndF(5 - 2 + 1)) = LFR(4) = MaxF - (MaxF - MinF) * ((2 - 1) / (4)) = 0.75
    • Untuk rr = 3: LFR(IndF(5 - 3 + 1)) = LFR(3) = MaxF - (MaxF - MinF) * ((3 - 1) / (4)) = 0.5
    • Untuk rr = 4: LFR(IndF(5 - 4 + 1)) = LFR(2) = MaxF - (MaxF - MinF) * ((4 - 1) / (4)) = 0.25
    • Untuk rr = 5: LFR(IndF(5 - 5 + 1)) = LFR(1) = MaxF - (MaxF - MinF) * ((5 - 1) / (4)) = 0.0
        Hasil:
      • LFR = [0.0, 0.25, 0.5, 0.75, 1.0]

          

Fungsi RouletteWheel ini merupakan implementasi dari metode pemilihan berbasis roda roulette, yang digunakan dalam algoritma genetik untuk memilih individu dari populasi berdasarkan nilai fitness mereka. Metode ini memberikan probabilitas pemilihan yang lebih tinggi kepada individu dengan fitness yang lebih tinggi.

Mari kita bahas setiap bagian dari kode tersebut:

function Pindex = RouletteWheel(UkPop, LinearFitness)
  • UkPop: Jumlah individu dalam populasi.
  • LinearFitness: Vektor yang berisi nilai fitness baru dari setiap individu, hasil dari proses skala linear.

Proses dalam Fungsi

  1. Hitung Jumlah Fitness:

    JumFitness = sum(LinearFitness);
    • JumFitness: total dari semua nilai fitness dalam LinearFitness.
    • Digunakan untuk menghitung probabilitas kumulatif masing-masing individu.

  2. Inisialisasi Variabel:

    KumulatifFitness = 0;
    RN = rand;
    ii = 1;
    • KumulatifFitness: menyimpan jumlah kumulatif fitness yang akan dibandingkan dengan angka acak.
    • RN: angka acak yang dihasilkan dari distribusi uniform [0,1], digunakan untuk menentukan individu yang terpilih.
    • ii: indeks yang digunakan untuk iterasi melalui populasi.

  3. Pemilihan Berdasarkan Roda Roulette:

    while ii <= UkPop
      KumulatifFitness = KumulatifFitness + LinearFitness(ii);
      if (KumulatifFitness / JumFitness) > RN
        Pindex = ii;
        break;
      end
      ii = ii + 1;
    end
  • Loop: Iterasi melalui setiap individu dalam populasi (ii dari 1 sampai UkPop).
    Tambahkan nilai fitness individu saat ini (LinearFitness(ii)) ke KumulatifFitness.
    • Hitung proporsi kumulatif fitness terhadap total fitness (KumulatifFitness / JumFitness).
    • Jika proporsi kumulatif ini melebihi angka acak RN, individu saat ini (ii) dipilih dan loop dihentikan dengan break.
    • Jika tidak, lanjutkan ke individu berikutnya (ii = ii + 1).

Penjelasan Metode Roda Roulette

  • Roda Roulette: Metode ini bekerja seperti roda roulette dalam permainan kasino, di mana bagian dari roda sesuai dengan probabilitas proporsional individu dalam populasi.
  • Proporsi Kumulatif: KumulatifFitness / JumFitness adalah probabilitas kumulatif yang menggambarkan berapa bagian dari total fitness yang telah "dilewati" saat mengiterasi.
  • Pemilihan Individu: Angka acak RN membagi total fitness menjadi beberapa segmen. Jika proporsi kumulatif melebihi RN, individu yang terpilih adalah individu yang saat ini sedang diiterasi.

Contoh

Misalkan ada 4 individu dengan nilai fitness sebagai berikut:

  • LinearFitness: [10, 20, 30, 40]
  • UkPop: 4

  1. Hitung Total Fitness:

    JumFitness = sum([10, 20, 30, 40]) = 100;

  2. Generate Random Number:

    RN = rand; % Misalkan RN = 0.65

  3. Iterasi dan Kumulatif Fitness:

    • Individu 1:
      • KumulatifFitness = 10
      • KumulatifFitness / JumFitness = 10 / 100 = 0.10 (0.10 < 0.65)
      • Lanjutkan ke individu berikutnya.
    • Individu 2:
      • KumulatifFitness = 10 + 20 = 30
      • KumulatifFitness / JumFitness = 30 / 100 = 0.30 (0.30 < 0.65)
      • Lanjutkan ke individu berikutnya.
    • Individu 3:
      • KumulatifFitness = 30 + 30 = 60
      • KumulatifFitness / JumFitness = 60 / 100 = 0.60 (0.60 < 0.65)
      • Lanjutkan ke individu berikutnya.
    • Individu 4:
      • KumulatifFitness = 60 + 40 = 100
      • KumulatifFitness / JumFitness = 100 / 100 = 1.00 (1.00 > 0.65)
      • Individu 4 terpilih karena proporsi kumulatif melebihi RN.


Ringkasan

Fungsi RouletteWheel memilih individu dari populasi berdasarkan nilai fitness mereka menggunakan metode pemilihan berbasis roda roulette. Individu dengan fitness lebih tinggi memiliki probabilitas lebih besar untuk dipilih. Metode ini memungkinkan setiap individu dalam populasi memiliki kesempatan untuk dipilih sesuai dengan kontribusi fitness mereka.


          

Fungsi PindahSilang ini merupakan implementasi dari operasi crossover (atau pemindahan silang) dalam algoritma genetik. Tujuannya adalah untuk menghasilkan individu baru (anak) dengan menggabungkan bagian-bagian dari dua individu orang tua (Bapak dan Ibu). Operasi ini merupakan langkah penting dalam algoritma genetik untuk menciptakan variasi genetik dan mengeksplorasi solusi baru.

Mari kita bahas kode fungsi PindahSilang secara rinci:

function Anak = PindahSilang(Bapak, Ibu, JumGen)

  • Bapak: Kromosom individu pertama (orang tua) yang akan digunakan dalam crossover.
  • Ibu: Kromosom individu kedua (orang tua) yang akan digunakan dalam crossover.
  • JumGen: Jumlah gen dalam setiap kromosom, yang merupakan panjang dari kromosom Bapak dan Ibu.

Proses dalam Fungsi

  1. Membangkitkan Titik Potong:

    TP = 1 + fix(rand * (JumGen - 1));
    • TP: Titik potong untuk crossover, yang ditentukan secara acak antara 1 dan JumGen-1. Titik ini adalah tempat di mana kromosom akan dipotong dan digabungkan.
    • rand menghasilkan angka acak antara 0 dan 1.
    • fix(rand * (JumGen - 1)) menghasilkan angka acak bulat antara 0 dan JumGen - 2.
    • Menambahkan 1 memastikan titik potong berada dalam rentang 1 hingga JumGen-1.

  2. Menghasilkan Anak dari Crossover:

    Anak(1, :) = [Bapak(1:TP) Ibu(TP+1:JumGen)];
    Anak(2, :) = [Ibu(1:TP) Bapak(TP+1:JumGen)];

  • Anak 1: Menggabungkan bagian depan dari Bapak hingga titik potong TP dengan bagian belakang dari Ibu setelah titik potong TP.
    • Bapak(1:TP) mengambil gen dari posisi 1 hingga TP dari kromosom Bapak.
    • Ibu(TP+1:JumGen) mengambil gen dari posisi TP+1 hingga akhir kromosom Ibu.
    • Anak(1, :) menyimpan hasil gabungan ini sebagai kromosom pertama dari anak.

  • Anak 2: Menggabungkan bagian depan dari Ibu hingga titik potong TP dengan bagian belakang dari Bapak setelah titik potong TP.

    Ibu(1:TP) mengambil gen dari posisi 1 hingga TP dari kromosom Ibu.
    • Bapak(TP+1:JumGen) mengambil gen dari posisi TP+1 hingga akhir kromosom Bapak.
    • Anak(2, :) menyimpan hasil gabungan ini sebagai kromosom kedua dari anak.

Contoh

Misalkan kita memiliki dua kromosom orang tua berikut:

  • Bapak: [1, 2, 3, 4, 5, 6, 7, 8]
  • Ibu: [8, 7, 6, 5, 4, 3, 2, 1]
  • JumGen: 8

  1. Membuat Titik Potong:

    Misalkan TP = 4.

  2. Menghasilkan Anak:

  • Anak 1:

    Bagian depan dari Bapak hingga TP: [1, 2, 3, 4]
    • Bagian belakang dari Ibu setelah TP: [5, 4, 3, 2, 1]
    • Gabungan: [1, 2, 3, 4, 5, 4, 3, 2]

  • Anak 2:

    Bagian depan dari Ibu hingga TP: [8, 7, 6, 5]
    • Bagian belakang dari Bapak setelah TP: [6, 7, 8]
    • Gabungan: [8, 7, 6, 5, 6, 7, 8, 1]


Ringkasan

Fungsi PindahSilang menggunakan metode crossover satu titik untuk menggabungkan gen dari dua individu orang tua (Bapak dan Ibu) untuk menghasilkan dua individu anak. Titik potong dipilih secara acak, dan gen sebelum titik potong diambil dari satu orang tua, sedangkan gen setelah titik potong diambil dari orang tua lainnya. Ini memungkinkan eksplorasi solusi baru dalam ruang pencarian algoritma genetik dan memperkenalkan variasi dalam populasi.


          


          Untuk menampilkan grafis 2D dari AG.
          Syntax-nya sebagai berikut :



           








     
    Terdapat tiga variabel utama yang harus ditentukan oleh user, yaitu: 
  1. UkPop (30-1000)
  2. Psilang (0,6-0,9)
  3. Pmutasi (1/jumlah gen)
%===============================================================================
% Mencari parameter optimal: ukuran populasi dan probabilitas mutasi
%
% Pencarian parameter optimal dilakukan dengan mengkombinasikan kedua
% parameter tersebut. Dalam observasi ini, digunakan empat nilai untuk
% masing-masing parameter, sehingga diperoleh 16 kombinasi.
% Nilai untuk kedua parameter adalah sebagai berikut:
% - UkPop: 50, 100, 200, dan 400
% - Pmutasi: 0.01, 0.05, 0.1, dan 0.2
%===============================================================================
clc % Me-refresh command window
clear all % Menghapus semua semua variabel yang sedang aktif
Nvar = 2; % Jumlah variabel pada fungsi yang dioptimasi
Nbit = 10; % Jumlah bit yang mengkodekan satu variabel
JumGen = Nbit*Nvar; % Jumlah gen dalam kromosom
Rb = -5.12; % Batas bawah interval
Ra = 5.12; % Batas atas interval
Psilang = 0.8; % Probabilitas pindah silang
MaxJumInd = 60000; % Jumlah individu maksimum yang dievaluasi
BilKecil = 10^-1; % Digunakan untuk menghindari pembagian dengan 0
Fthreshold = 1/BilKecil; % Threshold untuk nilai Fitness
Bgraf = Fthreshold; % Untuk menangani tampilan grafis
ObUkPop = [50 100 200 400]; % Ukuran populasi yang diobservasi
ObPmutasi = [0.01 0.05 0.1 0.2]; % Probabilitas mutasi yang diobservasi
ObData = []; % Data hasil observasi
for ukp=1:length(ObUkPop),
UkPop = ObUkPop(ukp);
MaxG = fix(MaxJumInd/UkPop);
for pm=1:length(ObPmutasi),
Pmutasi = ObPmutasi(pm);
for observasi=1:10,
UkPop, Pmutasi, observasi
% Inisialisasi populasi
Populasi = InisialisasiPopulasi(UkPop,JumGen);
% Loop evolusi
for generasi=1:MaxG,
x = DekodekanKromosom(Populasi(1,:),Nvar,Nbit,Ra,Rb);
Fitness(1) = EvaluasiIndividu(x,BilKecil);
MaxF = Fitness(1);
MinF = Fitness(1);
IndeksIndividuTerbaik = 1;
for ii=2:UkPop,
Kromosom = Populasi(ii,:);
x = DekodekanKromosom(Kromosom,Nvar,Nbit,Ra,Rb);
Fitness(ii) = EvaluasiIndividu(x,BilKecil);
if (Fitness(ii) > MaxF),
MaxF = Fitness(ii);
IndeksIndividuTerbaik = ii;
BestX = x;
end
if (Fitness(ii) < MinF),
MinF = Fitness(ii);
end
end
TempPopulasi = Populasi;
% Elitisme:
% - Buat satu kopi kromosom terbaik jika ukuran populasi ganjil
% - Buat dua kopi kromosom terbaik jika ukuran populasi genap
if mod(UkPop,2)==0, % ukuran populasi genap
IterasiMulai = 3;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
TempPopulasi(2,:) = Populasi(IndeksIndividuTerbaik,:);
else % ukuran populasi ganjil
IterasiMulai = 2;
TempPopulasi(1,:) = Populasi(IndeksIndividuTerbaik,:);
end
LinearFitness = LinearFitnessRanking(UkPop,Fitness,MaxF,MinF);
% Roulette-wheel selection dan pindah silang
for jj=IterasiMulai:2:UkPop,
IP1 = RouletteWheel(UkPop,LinearFitness);
IP2 = RouletteWheel(UkPop,LinearFitness);
if (rand < Psilang),
Anak = PindahSilang(Populasi(IP1,:),Populasi(IP2,:),JumGen);
TempPopulasi(jj,:) = Anak(1,:);
TempPopulasi(jj+1,:) = Anak(2,:);
else
TempPopulasi(jj,:) = Populasi(IP1,:);
TempPopulasi(jj+1,:) = Populasi(IP2,:);
end
end
% Mutasi dilakukan pada semua kromosom
for kk=IterasiMulai:UkPop,
TempPopulasi(kk,:) = Mutasi(TempPopulasi(kk,:),JumGen,Pmutasi);
end
% Generational Replacement: mengganti semua kromosom sekaligus
Populasi = TempPopulasi;
if MaxF >= Fthreshold,
JumIndData(observasi) = generasi*UkPop;
MaxFData(observasi) = MaxF;
break;
else
if generasi == MaxG,
JumIndData(observasi) = MaxG*UkPop;
MaxFData(observasi) = MaxF;
end
end
end % loop evolusi
end % loop observasi
ObData = [ObData ; [UkPop Pmutasi mean(MaxFData) mean(JumIndData)]];
end
end
save ObData.mat ObData
clc % me-refresh layar
disp(['Mencari nilai optimal: Ukuran Populasi dan Prob. Mutasi ']);
disp(['Jumlah maksimum individu yang dievaluasi adalah ', num2str(MaxJumInd)]);
disp([' ']);
disp(['--------------------------------------------------------']);
disp(['Ukuran Probabilas Rata-rata Rata-rata ']);
disp(['Poulasi mutation Fitness Jumlah individu']);
disp(['--------------------------------------------------------']);
for ii=1:length(ObData(:,1)),
disp([' ', num2str(ObData(ii,1)),' ', num2str(ObData(ii,2)), ...
' ', num2str(ObData(ii,3)),' ', num2str(ObData(ii,4))]);
end
disp(['--------------------------------------------------------']);
    






Hana

Diposting oleh Hana

Posting Komentar

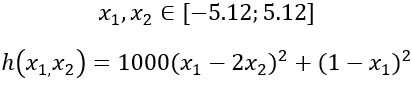
0 Komentar